wildcornstalk
New member
- Joined
- Jun 28, 2011
- Messages
- 8
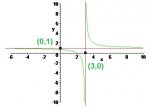
find the equations of both the horizontal and vertical asymptotes of the rational function.
a. f(x)=(5x-1)/(x^2+9) i have the vertical as x=-3 and the horizontal as y=0
b. f(x)=(2x^2+8)/(x-1) vertical is x=1 and there is no horizontal.
my question was what exactly do they mean by finding the equation? And also, if I have a graph with points how would I find the equation with only that information. My book doesnt explain very well.
Thank you for your time!
a. f(x)=(5x-1)/(x^2+9) i have the vertical as x=-3 and the horizontal as y=0
b. f(x)=(2x^2+8)/(x-1) vertical is x=1 and there is no horizontal.
my question was what exactly do they mean by finding the equation? And also, if I have a graph with points how would I find the equation with only that information. My book doesnt explain very well.
Thank you for your time!