Arithmetic Interference Pattern

[Agent Smith]

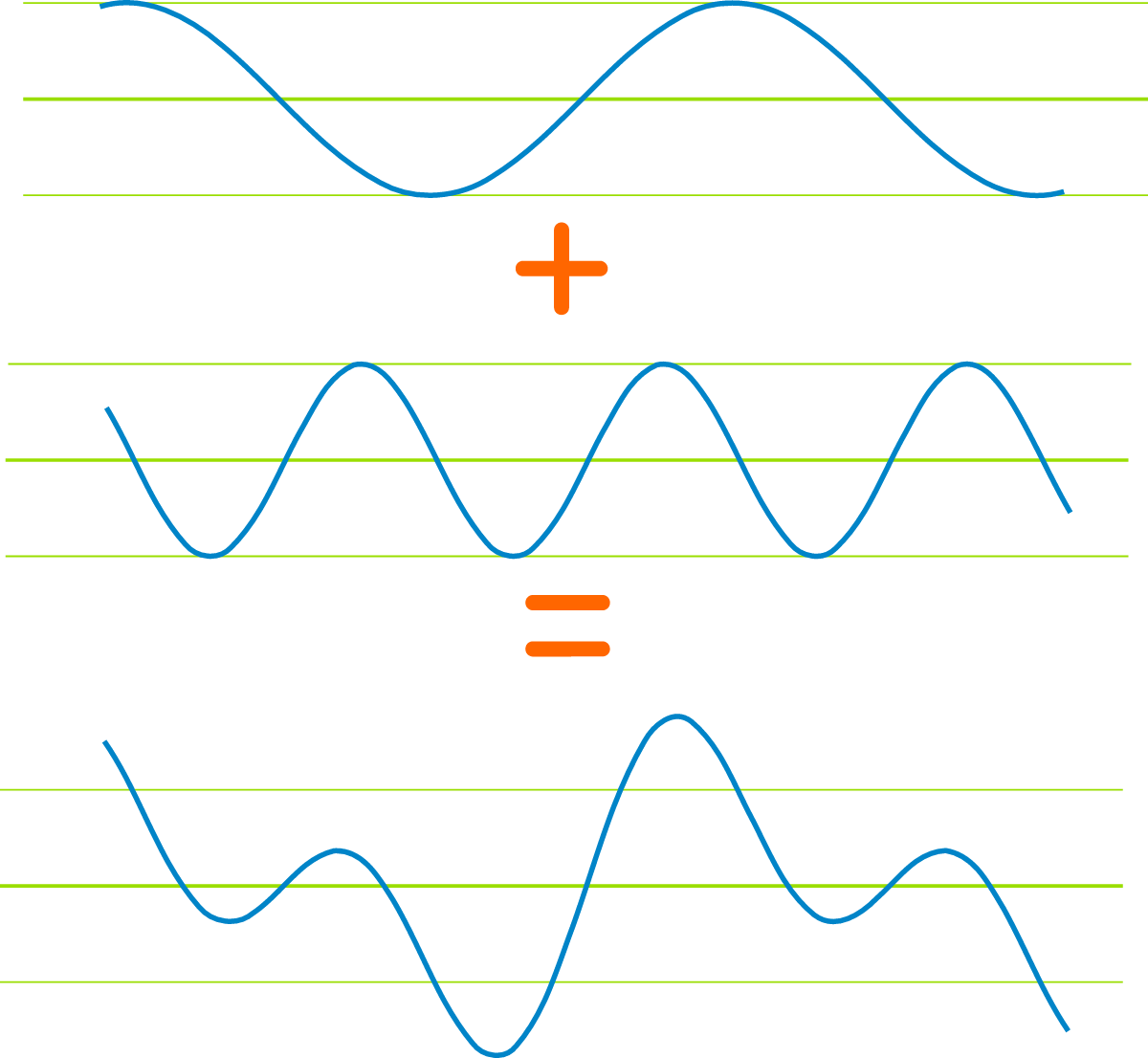
I hope the diagram is self-explanatory. I didn't we could express multiples of a number with a trig function. I've used the cosine function here. Each multiple of a number [imath]n[/imath], I've used 3 and 5, appears as the [imath]x[/imath] value for which [imath]y = \cos x = 1[/imath] (the cosine function's periods have been recalibrated to 3 and 5).

As you can see we have peaks/troughs, categorizable into local & global. I know that the global zeniths are common multiples, they resonate as it were. So, the maxima are x = {15, 45, 60, ...}.

An interference pattern for numerical waves.

Using simple functions:

f(x) = 3x
g(x) = 5x

The plot above corresponds to h(x) = [imath]\frac {f(x)g(x)}{x} = f(\sqrt x)g(\sqrt x)[/imath]

What are the other minima/maxima?
Anything else worth noting?

 

[fresh_42]

View attachment 36880

I hope the diagram is self-explanatory.

I'm afraid not here. You can do a lot of funny things with trig functions. An entire mathematical concept (Fourier Transformations) is based on them. It is particularly important in signal theory, how surprising!

f(x) = 3x
g(x) = 5x

The plot above corresponds to h(x) = [imath]\frac {f(x)g(x)}{x} = f(\sqrt x)g(\sqrt x)[/imath]

What are the other minima/maxima?

You get the local extrema of a function [imath] h(x) [/imath] by looking where the tangent to the function graph is horizontal. This means, where it has no slope, i.e. where [imath] h'(x)=0. [/imath] However, it might happen that you can only find all such locations by numerical methods because products and square roots are hard to handle in equations.

Anything else worth noting?

I do not see anything.

 

[blamocur]

What are the other minima/maxima?

Take the derivative, then convert the sum of trig functions to a product and you'll get an explicit solution to this question.

 

[Agent Smith]

Take the derivative, then convert the sum of trig functions to a product and you'll get an explicit solution to this question.

Derivative = 0, after that it's all blank.

Anyway, the functions I built (rudimentary, but I ain't no math prof). are supposed to pick up resonance (for integers, they're basically x = 3n = 5m). I was wondering if the other peaks are also similar in character, one of 'em occurs at [imath]x = 7.5 = 3 \cdot 2.5 = 5 \cdot 1.5[/imath].

As for the troughs, I haven't examined them as of yet.

Too, was wondering if this is another modus of understanding/analyzing numbers. How do other number (set as periods of sine) combinations look? Do the waves exhibit different, (easily) identifiable patterns for composite-composite and prime-composite and prime-prime combinations. Incidentally, the example I chose is prime-prime. We could study other classes of numbers too, but of course we'd need to augment my simple trig functions appropriately, customizing them for the task at hand.

The global maxima, patently obvious what they are, can, for example, be used to find LCM. Not offering anything better, just different.

The local max and min look interesting; at the moment all I can say is they too seem to be common multiples (the local maxima), but for [imath]3n = 5n = x[/imath], n is not an integer. What can be said is that if [imath]3 \cdot 15 = 5 \cdot 9 = 45[/imath], there'll be a relative max at x = 4.5.

We could, could we?, also use these trig functions to model cyclic phenomena. Maybe I'm being too optimistic. Yes/no/both/neither/stupido!?

 

[blamocur]

We could, could we?, also use these trig functions to model cyclic phenomena. Maybe I'm being too optimistic. Yes/no/both/neither/stupido!?

I don understand this question. All I was suggesting is that for the sum of two cosines one can find explicit formulae for min/max points.

 

[Dr.Peterson]

We could, could we?, also use these trig functions to model cyclic phenomena. Maybe I'm being too optimistic. Yes/no/both/neither/stupido!?

Did you try looking up Fourier transforms, as suggested in the first response? That (or, more directly, the Fourier series) is your "yes" answer! This uses sums like yours (with more terms) to construct virtually any periodic function.

Here is a friendly introduction:

Fourier Series

Math explained in easy language, plus puzzles, games, quizzes, videos and worksheets. For K-12 kids, teachers and parents.

www.mathsisfun.com

(rudimentary, but I ain't no math prof)

It may help us interact with you better if you tell us a little about what mathematical background you do have, so we can know what to expect of you.

 

[Agent Smith]

Did you try looking up Fourier transforms, as suggested in the first response? That (or, more directly, the Fourier series) is your "yes" answer! This uses sums like yours (with more terms) to construct virtually any periodic function.

Here is a friendly introduction:

Fourier Series

Math explained in easy language, plus puzzles, games, quizzes, videos and worksheets. For K-12 kids, teachers and parents.

www.mathsisfun.com

It may help us interact with you better if you tell us a little about what mathematical background you do have, so we can know what to expect of you.

Fourier transforms, heard of them. Question, have they been applied to number theory, like I suggested. It seems we might have to tolerate some information loss, but its the, for lack of a better term, character of the interference between different wave-numbers that I'm interested in.

The local maxima seem to occur at whole number multiples of 3 in my example; having a higher frequency, and maxxing out, they dominate the wave. The local minima are half-way points between the whole number multiples and here too, due to higher frequency, 3 rules the roost. Since 5 is asymmetrically placed between two multiples of 3, viz. 3 and 6, we never see [imath]f(x) + g(x) = 0[/imath].

 

[fresh_42]

Fourier transforms, heard of them. Question, have they been applied to number theory, ...

Yes, in their discrete version, e.g. in cryptography.

... like I suggested.

No. However, that "no" might be because I have no idea what you are going to end up with.