Area underneath curve

[lamaclass]

How would a problem like this be set up?

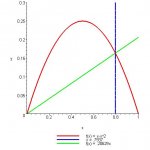
There is a line through the origin that divides the region bounded by the parabola y=x-x[sup:1arbbe41]2[/sup:1arbbe41] and the x-axis into two regions with equal area. What is the slope of that line?

 

[Aladdin]

------------------

http://mathcentral.uregina.ca/QQ/database/QQ.09.07/h/james8.html

Hope that this will help.

 

[BigGlenntheHeavy]

\(\displaystyle First\ note\that \ total \ area \ under \ f(x) \ is \ \frac{1}{6}, \ observe \ graph.\)

[attachment=0:1674ka0m]mno.jpg[/attachment:1674ka0m]

\(\displaystyle Now, \ if \ we \ let \ x \ = \ k, \ we \ get \ \frac{1}{12} \ = \ \int_{0}^{k}[x-x^{2}-mx}]dx, \ \implies \ \frac{-k^{3}}{3}-\frac{k^{2}(m-1)}{2} \ = \ \frac{1}{12}.\)

$\displaystyle Ergo, \ mk \ = \ k-k^{2} \ \implies \ k \ = \ 0 \ or \ k \ = \ 1-m$

$\displaystyle Hence, \ -\frac{(1-m)^{3}}{3}-\frac{(1-m)^{2}(m-1)}{2} \ = \ \frac{1}{12}, \ m \ = \ \bigg(1-\frac{2^{2/3}}{2}\bigg) \ = \ .20629$

$\displaystyle Post \ Script: \ Thank \ you \ Aladdin \ for \ your \ aid, \ as \ it \ made \ it \ easier \ to \ solve \ this \ problem.$

$\displaystyle I \ didn't \ have \ to \ think.$

 

[lamaclass]

Thank you both very much!