Area under a polar curve

[MarkSA]

Hello,

I have a problem:

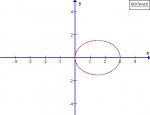
Sketch the curve and find the area that it encloses, given:
r = 3cos(theta)

Well, I sketched it (rather graphed it) and it's a circle, but half of the circle lies below the x-axis. I know I can find the area of a circle with just pi*r^2 but I decided to work it out with integrals.

I found that the limits to create the circle are from 0 to pi. I thought since half of the circle lies below the x-axis, taking the integral from 0 to pi would give me an answer of '0' since that would be the 'net area' (+half above added to -half below). However, doing this gave me the right answer of 9pi/4 which confuses me since half of the area lies below the x-axis. Yet in other problems it appears that the integral has to be split up to handle areas beneath the x-axis and give the total area rather than net area properly. Why is this? Can you help explain?

 

[galactus]

This should give you the area:

\(\displaystyle \frac{1}{2}\int_{0}^{\pi}(3cos({\theta}))^{2}d{\theta}\)

Chexk it against \(\displaystyle {\pi}r^{2}\)

 

[MarkSA]

Thanks, so when dealing with polar curves, it doesn't matter if portions of them are below the x-axis?

 

[galactus]

I'm sorry. That limit should've been from 0 to Pi, not 2Pi. I fixed it.