Area of an integral with respect to y

[lamaclass]

I just wanted to make sure I understand what this problem is asking for:

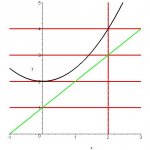
The integral below represents the area of a region between two functions, x = 0 and x =2.

IN, limits 0 and 2, (1/2x[sup:1mwles0i]2[/sup:1mwles0i] + 2) - (x + 1) dx

A) Sketch the region whose area is given by the integral

B) Set up an integral(s) for the area by integrating with respect to y.

I figured out how to do part A however for part B I was unsure of how many integrals to use. It looked like three maybe but I'm not for sure. Otherwise I know you can solve for x like this:

x = y+1

x = sq rt. (2y-4)

The areas that I found were:

Area I: IN, limits -2 and 2, (2 - sq rt. 2y-4) dy

Area II: 2 square units

Area III: IN, limits -1 and 1, y + 1 dy

Is this right?

 

[BigGlenntheHeavy]

\(\displaystyle A \ = \ \int_{0}^{2}\bigg[(\frac{x^{2}}{2}+2)-(x+1)\bigg]dx \ = \ \frac{4}{3}, \ I'm \ assuming \ this \ is \ right.\)

\(\displaystyle Then, \ A \ = \ \int_{3}^{4}(2-\sqrt{2y-4})dy+\int_{2}^{3}[(y-1)-\sqrt{2y-4}]dy+\int_{1}^{2}(y-1)dy \ = \ \frac{4}{3}\)

\(\displaystyle See \ Graph\)

[attachment=0:1o0x02vb]mno.jpg[/attachment:1o0x02vb]

 

[BigGlenntheHeavy]

[attachment=0:1360xt1h]pqr.jpg[/attachment:1360xt1h]

\(\displaystyle Look \ at \ the \ above \ plot.\)

\(\displaystyle It \ is \ obvious \ that \ the \ blue \ rectangle \ has \ an \ area \ of \ A \ = \ lw \ = \ (2)(1) \ = \ 2 \ sq. \ units\)

\(\displaystyle Now, \ integrating \ with \ respect \ to \ x \ yields: \ A \ = \ \int_{1}^{3}(4-3)dx \ = \ 2 \ sq. \ units\)

\(\displaystyle and \ integrating \ with \ respect \ to \ y \ yields: \ A \ = \ \int_{3}^{4}(3-1)dy \ = \ 2 \ sq. \ units.\)