XYZW is a rectangle with:
YZ = 10cm
YP = 8cm
ZP = 6cm
Determine the area of XYZW.
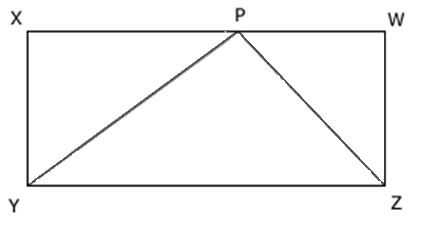
So, what I figured is that because it is a rectangle, I could use the pythagorean theorem, but the problem is, I don't have the necessary side lenghts and I can't think of any other way to do it...
YZ = 10cm
YP = 8cm
ZP = 6cm
Determine the area of XYZW.

So, what I figured is that because it is a rectangle, I could use the pythagorean theorem, but the problem is, I don't have the necessary side lenghts and I can't think of any other way to do it...
