akoaysigod
Junior Member
- Joined
- Oct 5, 2009
- Messages
- 65
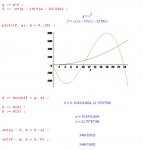
Suppose the graph of a cubic polynomial intersects the parabola y=x^2 when x=0, x=a, and x=b where 0 < a < b. If the two regions between the curves have the same area, how is b related to a?
So far I know the equation of the polynomial will be f(x)=x(x-a)(x-b) because it gives the zeroes of the equation
in the problem. I'm just not sure where to go from here. If I set it up into an integral that would find the area it would be
int[0,a] f(x)-x^2 + int[a,b] x^2-f(x) where f(x)=x(x-a)(x-b)
Which doesn't get me anywhere, and I'm not even sure I can assume which of those functions comes first. Any hints? I'd like to be able to do this on my own but I'm not entirely sure which directions I should I take with this. I could also set the two equal to each other but that also doesn't get me anywhere.
Thanks
Also, is there anyway for me to type integrals and such so they look like they would hand written? Writing it out like this is confusing to look at.
So far I know the equation of the polynomial will be f(x)=x(x-a)(x-b) because it gives the zeroes of the equation
in the problem. I'm just not sure where to go from here. If I set it up into an integral that would find the area it would be
int[0,a] f(x)-x^2 + int[a,b] x^2-f(x) where f(x)=x(x-a)(x-b)
Which doesn't get me anywhere, and I'm not even sure I can assume which of those functions comes first. Any hints? I'd like to be able to do this on my own but I'm not entirely sure which directions I should I take with this. I could also set the two equal to each other but that also doesn't get me anywhere.
Thanks
Also, is there anyway for me to type integrals and such so they look like they would hand written? Writing it out like this is confusing to look at.