Area bound by the 2 curves y=(1/12)x^2 + 7/12, y=1/2x

[fred2028]

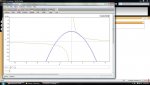
The question reads:

Find the area bound by the curves

y = -(1/12)x^2 + 7/12 and
y = 1/2x

No intervals nor any other information is given.
The textbook says to take integral of the upper curve minus the lower curve, but how do you determine which is the upper and which is the lower without graphing?

Secondly, so I graphed it, and the graphs are in the attached image. "The area bound by the 2 curves": Wouldn't this be infinity since, in the 3rd quadrant, the area between the 2 curves approaches infinity as y approaches negative infinity?

 

[galactus]

Re: Area bound by the 2 curves

They more than likely mean the area in the first quadrant.

 

[fred2028]

Re: Area bound by the 2 curves

They more than likely mean the area in the first quadrant.

OK, so let's assume it's in quadrant 1. How would you determine which is "the upper curve" and which is "the lower curve" without graphing?

 

[fasteddie65]

Re: Area bound by the 2 curves

You could solve the system and find the intersection points. I find that (1, 1/2) and (2, 1/4) are the points of intersection.
Now take a value 1 < x < 2; let's choose x = 1.5.

For the first curve, y = 0.395... or 19/48; for the second, y = 1/3. Since 1/3 < 19/48, the first curve is the upper one.