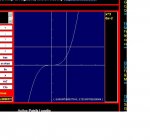
Hello here are the equations:
y = x^2 - 4x
y = x - 4
The bounds are [1,4]
I set this up like this:
(integral) [1,4] (x - 4) - (x^2 - 4x)
(integral) [1,4] (-x^2 + 5x - 4)
Am i correct so far?
------------
Also i have another problem:
f(x)= sin(x) g(x) = cos(x) (pi)/4 < x < 5(pi)/4
I need to solve for each intersecting point... but i forgot how I'd go about manipulating that.
y = x^2 - 4x
y = x - 4
The bounds are [1,4]
I set this up like this:
(integral) [1,4] (x - 4) - (x^2 - 4x)
(integral) [1,4] (-x^2 + 5x - 4)
Am i correct so far?
------------
Also i have another problem:
f(x)= sin(x) g(x) = cos(x) (pi)/4 < x < 5(pi)/4
I need to solve for each intersecting point... but i forgot how I'd go about manipulating that.