username01
New member
- Joined
- May 5, 2014
- Messages
- 2
can anyone help with the following question?:
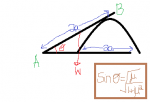
The diagram shows a uniform rod AB of weight W and length 2a. The rod rests with a on rough horizontal ground and leans against a rough fixed prism of semicircular cross-section of radius a. the coefficient of friction at both contacts is mu. When friction is limiting the rod makes an angle theta with the horizontal. show that
sin(theta)=sqrt((mu/(1+(mu squared)))
Question is from AQA A-level maths M2 textbook, ex 2D, Q9, where there is also a diagram (and the final line is formatted better and easier to read!) if anyone has this book and it helps.
thanks
The diagram shows a uniform rod AB of weight W and length 2a. The rod rests with a on rough horizontal ground and leans against a rough fixed prism of semicircular cross-section of radius a. the coefficient of friction at both contacts is mu. When friction is limiting the rod makes an angle theta with the horizontal. show that
sin(theta)=sqrt((mu/(1+(mu squared)))
Question is from AQA A-level maths M2 textbook, ex 2D, Q9, where there is also a diagram (and the final line is formatted better and easier to read!) if anyone has this book and it helps.
thanks