I have a few more problems, and I really need to make sure I know how to do this! My AP calculus class uses relatively simple calculus, I assume, since we didn't even learn Integration by Parts; so any assistance and showing every step will reaaaalllly help. :]
Find the volume of a solid obtained by rotating the region bounded by the curves y=x[sup:1wkht64s]3[/sup:1wkht64s], y=0, and x=1 about the line x=2. Sketch a graph.
I sketched it, I've got something that looks like a small volcano.
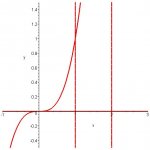
Find the volume of a solid obtained by rotating the region bounded by the curves y=x[sup:1wkht64s]3[/sup:1wkht64s], y=0, and x=1 about the line x=2. Sketch a graph.
I sketched it, I've got something that looks like a small volcano.