Application of Integration Question! Help!

[br1tt204]

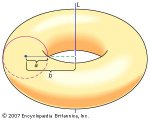
This may be hard to visualize without a graph, so I apologize in advance, but here is my question:

There is a circle with radius 'b' that is 'a' units away from the y-axis. if the circle is rotated about the y-axis, how do you find the volume of the doughnut that is formed? (assume that b<a)

I would even appreciate a jump start! Anything, really! Thank you in advanced!

 

[wjm11]

There is a circle with radius 'b' that is 'a' units away from the y-axis. if the circle is rotated about the y-axis, how do you find the volume of the doughnut that is formed?

Use the washer method. There is a nice example here:

http://www-math.mit.edu/~djk/18_01/chap ... ion03.html

 

[galactus]

There is also something called the 'Theorem of Pappus' that works well with finding the volume of the 'doughnut'

$\displaystyle \text{volume=(area of R)(distance traveled by the centroid)}$

Say we have a torus (doughnut) and we want to find its volume. We do this by rotating the circle around the L-axis.

By symmetry, the centroid of a circle is its radius point. Say it has radius a.

The circle is a distance, b, from the L-axis we are revolving about. This distance traveled around the L-axis is $\displaystyle 2{\pi}b$

Therefore, the volume of the torus is $\displaystyle (\overbrace{2{\pi}b}^{\text{distance traveled by center of circle}})(\underbrace{{\pi}a^{2}}_{\text{area of circle being revolved}})=2{\pi}^{2}ba^{2}$

 

[BigGlenntheHeavy]

Volume of torus: Shell method.

$\displaystyle I \ am \ assuming \ that \ the \ equation \ of \ the \ circle \ is \ (x-a)^{2}+y^{2} \ = \ b^{2}$

$\displaystyle Also \ one \ is \ not \ familiar \ with \ "The \ Theorem \ of \ Pappus" \ of \ Alexandria \ (ca. \ 300 \ A.D.)$

$\displaystyle Now \ the \ area \ of \ the \ circle \ is \ 2\int_{-b}^{b}\sqrt(b^{2}-x^{2})dx \ = \ \pi b^{2}.$

$\displaystyle Ergo, employing \ the \ shell \ method, \ p(x) \ = \ a, \ we \ have \ 4\pi\int_{-b}^{b}a\sqrt(b^{2}-x^{2}) \ dx \ = \ 2ab^{2}\pi^{2}.$