Application of Integration- help!

[tkvictim]

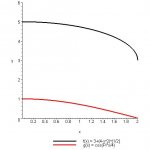
Directions: Calculators may not be used. Region W is bounded by f(x) = 3 + (4-x[sup:20zq42i5]2[/sup:20zq42i5])^[sup:20zq42i5]1/2[/sup:20zq42i5], g(x)=cos(pi/4x), x=0, x=2. What is the area of region W?

They give me an illustration of the graph, and I set up my integral as

S [0,2] 3 + (4-x[sup:20zq42i5]2[/sup:20zq42i5])^[sup:20zq42i5]1/2[/sup:20zq42i5] - cos(pi/4x) dx
Even though I'm not supposed to use my calculator.. I utilized the fnInt function and I got roughly 7.868, but the possible answers that are given to me are:

(a) 6.000
(b) 6 + pi - (pi/4)
(c) 6 + pi + (pi/4)
(d) 6 + 2pi - (4/pi)
(e) 6 + 2pi + (4/pi)

And none of them equate to the value that I got.. Can anyone tell me where I messed up? And how could I fix it without the help of my calculator? Haha

 

[BigGlenntheHeavy]

\(\displaystyle A \ = \ \int_{0}^{2}[f(x)-g(x)]dx \ = \ \int_{0}^{2}3dx+\int_{0}^{2}(4-x^2)^{1/2}dx-\int_{0}^{2}cos(\pi x/4)dx\)

\(\displaystyle A \ = \ 6+\pi-\frac{4}{\pi} \ \dot= \ 7.868, \ see \ graph \ bottomless \ pit \ ha,ha.\)

[attachment=0:1z8210qf]zzz.jpg[/attachment:1z8210qf]

 

[tkvictim]

That is really odd that the answer isn't listed in any of the choices they give me.. a typo on their part. Thank you. =)