Apply Cauchy's theorem to the function
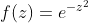and the sector of the circle
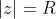bounded by a section of the real axis and a linear segment making the angle
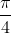with the real axis.
1. Show that the integral over the circular boundary tends to zero as R tends to infinity. Is it because [MATH] \left| e^{-z^2} \right| \leq 1 [/MATH]?
2. Show that
I can't seem to solve it. Looking it up, the websites refer to Fresnel but I haven't learned anything about it so I can't use that method.
1. Show that the integral over the circular boundary tends to zero as R tends to infinity. Is it because [MATH] \left| e^{-z^2} \right| \leq 1 [/MATH]?
2. Show that
I can't seem to solve it. Looking it up, the websites refer to Fresnel but I haven't learned anything about it so I can't use that method.