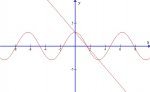
Let be the function given by f(x) = 3 cos x. The graph of f crosses the y-axis at point P and the x-axis at point Q.
Write an equation for the line passing through points P and Q
Point P(0,3)
Point Q(?/2, 0)
This is what I did
y-3=3 cos x(x-0)
y-3= -sin 3x(x^2-0)
This is what I got so far. I plugged in the values then took that derivative of that 3 cos x
Write an equation for the line passing through points P and Q
Point P(0,3)
Point Q(?/2, 0)
This is what I did
y-3=3 cos x(x-0)
y-3= -sin 3x(x^2-0)
This is what I got so far. I plugged in the values then took that derivative of that 3 cos x
Code:
| ,---.
| / \ y = f(x)
|/ \
|P = (0, 3) \
| \
| \
| Q = (pi/2, 0) \
----+------------------\--
| \
|