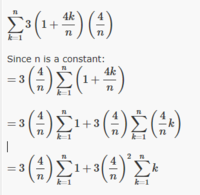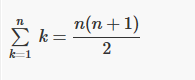Any help with this?

[takelight]

Express [∑(n) (k=1) [3(1+4k/n)]*(4/n)] as a closed form. (your answer will be in terms of n.

So this is my progress so far:
Attached below

I guess im missing the sum of 1 +3(4/n) I really don't know how to evaluate that.

 

[MarkFL]

As you did, I would bring all factors that are not a function of the index of summation out front:

[MATH]S=\frac{12}{n}\sum_{k=1}^{n}\left(1+\frac{4k}{n}\right)[/MATH]
And then:

[MATH]S=\frac{12}{n}\sum_{k=1}^{n}\left(1\right)+\frac{48}{n^2}\sum_{k=1}^{n}\left(k\right)[/MATH]
Can you proceed?

 

[takelight]

As you did, I would bring all factors that are not a function of the index of summation out front:

[MATH]S=\frac{12}{n}\sum_{k=1}^{n}\left(1+\frac{4k}{n}\right)[/MATH]
And then:

[MATH]S=\frac{12}{n}\sum_{k=1}^{n}\left(1\right)+\frac{48}{n^2}\sum_{k=1}^{n}\left(k\right)[/MATH]
Can you proceed?

How can you possible evaluate the sum (n)(k=1) of 1??? what does that sum return? That's the only part im missing I think.

 

[lev888]

How can you possible evaluate the sum (n)(k=1) of 1??? what does that sum return? That's the only part im missing I think.

Can you write it out if n=2? How about 3? See the pattern?

 

[MarkFL]

How many 1's would you have? What do you get when you add that many 1's?

 

[takelight]

Can you write it out if n=2? How about 3? See the pattern?

oh lmao. its just n. So like 1 times the n since it keeps adding one. Im stupid. D: