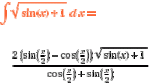First, to Subhotosh Khan: I noticed my typo immediately upon reading over my post after submission, but since my point only concerned the gargantuan size of Mathematica's output, not its content, I felt I needn't bother correcting it. What kind of fool am I?! In lay circles, a typo or two makes you a "regular guy". In mathematical circles--a pariah!! So, I heartily apologize for leading you astray, Subhotosh (if I may call you that). Incidentally, with your correction, Mathematica's Atrocity is now one digit more atrocious!
Now to the main purpose of this post. Probably surprisingly, I deliberately omitted from my first post the reason that actually impelled me to write about this subject! I did so because to have included it would have rendered it simply too long and complex. That first post raised essentially aesthetic objections to Mathematica's Monstrosities--contrasting one of their typical lumbering mammoths with an archetypal human creation, sleek and elegant like a Hitchcock blonde. And while mathematicians (and scientists too) justifiably greatly prize beauty and elegance in their equations--to the point of feeling that if they're not beautiful they must be wrong--in this case I have a more significant concern. I believe it's possible (I won't state it more strongly) that these Mathematica Anti-derivatives of Ill Repute will eventually have a detectable corrosive effect on math and, even more so, science. An absurd contention on the surface (and perhaps at its core, too!) but I want to present a brief argument and then get any feedback this intelligent and informed mathematical community might wish to provide.
First, I'm making two assumptions, both of which appear reasonable. 1)Due to the nature of the method Mathematica and its equivalents use to integrate, vastly-larger-than-human-produced anti-derivatives are routine, not anomalous, even with the simplifying algorithms I know they employ. 2)Mathematicians and scientists have been and will be increasingly reliant on Mathematica et. al., so that over time there will be a loss of "institutional memory" of how to integrate very complicated functions "the human way". The heuristics, the intuitions, the artistry that develops only through frequent practice from early on will fade away with the current generation's passing-- the rookies coming up will have supposedly more urgent and marketable mathematical skills to develop. Take a quick, savoring glance, while you still can, at the three different human (i.e. inventive) approaches of galactus, soroban, and subhotosh as each deftly harpooned the elusive integral that would so easily have wriggled away from lesser men--those lesser men will largely dominate our very near mathematical future. Skeptical that such precipitous erosion of a whole community's skills is possible? When the proposal to return to the moon was made a few years ago, a NASA scientist was asked why this second series of missions would take as long to consummate as the first, and he said that all the little unwritten tricks of the trip-to-the-moon trade had been institutionally forgotten and would have to be painstakingly relearned. Of course, there will always be a special few who almost mystically perceive the route to an anti-derivative, but most math and almost all day-to-day science will be performed by Saint Stephen of Mathematica's disciples.
So if these two assumptions are valid, the result will be that mathematicians and scientists will be "stuck" with Mathematica's Ungodly Octopi for functions that COULD have been integrated to compact anti-derivatives by humans. So how might this harm both math and science (especially the latter), as I so implausibly claim? In two ways.
1)Paul Dirac, creator of an equation as famous among physicists as it is unknown to the general public, said of his creation:"My equation is smarter than I am." He didn't elaborate, but I believe what he meant was that sometimes scientists ASSEMBLE equations-- perfectly understanding all the concepts involved and the relationships among them, the scientists symbolically represent what they already know, and poof!, there's the equation. But other times, scientists DERIVE equations mathematically, having only the most tenuous grasp of what's really going on physically, and not a glimmer of where it will end up mathematically. These mysterious new equations hold secrets about nature that can be pried loose for the scientists' edification--THESE equations are smarter than they are. (And sometimes the prying takes decades--Alan Guth is said to have discovered Big Bang Inflation lurking deep in the bowels of General Relativity about 60 years after its debut.) But the discerning of these hidden truths may well depend on the transparency of the equations, on their being as simple as possible a rendering of the relationship among the components--not exactly a description of an equation with the perhaps 20 extra terms of a Mathematica Monstrosity. The smartest equation in the world would have difficulty communicating with scientists through that!!
2)The second way Mathematica's Anti-derivatives Not Even Wolfram's Mother Could Love might do harm concerns those situations where you integrate the anti-derivative a second time, as from acceleration to velocity and then to distance. Or, alternatively, when you have what I'll call amnesic anti-derivatives, ones living in a new location, as just another algebraic term in a new larger equation, with no memory of their past life as an anti-derivative, and you must integrate that new equation. In either of these cases (and I'm sure there are others), Mathematica's Sprawling Swamps may well make the task impossible when it would be eminently doable if you had a neat human anti-derivative--everyone reading this has observed how quickly a little complexity renders a function unintegratable by anti-derivative, so that numerical procedures are necessary. And while numerical procedures are fine for solving a particular problem, they deny you the opportunity of creating and interrogating a new equation that's smarter than you are, and so the advance of science is again thwarted. Now, will the truly paradigm-doing-somersaults-not-merely-shifting science be affected by this? Will Ed Witten of the Institute for Advanced Studies fail to perfect String Theory for want of a compact anti-derivative? No. But there will be countless instances when little insights in everyday science are missed because final integrations couldn't be achieved or equations spoke but couldn't be heard, muffled by Mathematica's ruffians. Meanwhile, the mathematicians who could have created the necessary anti-derivatives will be busy testing non-trivial zeros of Bernie's zeta function or God knows what. By the way, regarding this second line of argument, I freely acknowledge my calculus is not yet sophisticated enough to do more than tentatively raise a few of many possibilities--that's why I'm eager to see responses from the knowledgeable, frequent posters, all you Sovereigns of the Infinitesimal Realm, who can affirm or pitilessly savage my argument, as its validity dictates.
In fact, I welcome comments from ANYONE who sees fit to comment. No one who visits a site like this would be unworthy of being heard.