another one I missed Help!!

[Belby]

Find the intersection of the line through the points (7, 7) and (4,2) with the line y=x. The point of intersection is (A,B) where A=? B=?.
I used y-y1=m(x-x1)
y-7=5/3(x-7)
y-7=5/3x-35/3
y=5/3x-14/3
y=3(5/3x-14/3)
y=9

This is wrong. Help!

 

[mmm4444bot]

y = 5/3x - 14/3 Your work is correct, up to this point.

Now, we have equations for two lines.

y = (5/3)x - 14/3

y = x

Since both of the righthand-side expressions above equal the same number (y), both of these expressions must equal one another at the point of intersection.

(5/3)x - 14/3 = x

You can find A and B from this equation. (Do you realize that A = B, since the intersection point (A, B) lies on the line y = x ?)

MY EDIT: Added clarification, and fixed transposition error.

 

[Belby]

I'm totally lost.

 

[mmm4444bot]

I'm totally lost.

I apologize; I could have been clearer.

We have two different lines. They intersect somewhere at a single point.

Since every point on the line y = x has equal x- and y-coordinates, the point of intersection with the other line must have equal x- and y-coordinates.

I'll upload an image, momentarily.

 

[mmm4444bot]

In the meantime, can you solve the following equation for x ?

(5/3)x - 14/3 = x

 

[Belby]

-4

 

[mmm4444bot]

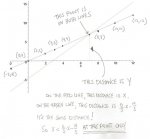
[attachment=0:3icfmd4g]4Belby.JPG[/attachment:3icfmd4g]

Double-click the image, to expand.

(Oh, the colors faded. The red line is the line with the labeled points.)

The red line is part of the graph of y = x .

The green line is part of the graph of y = (5/3)x - 14/3 .

Every point on the red line has coordinates (x, x).

At the point of intersection, the y-coordinate can be written two different ways.

It can be written as x.

It can be written as (5/3)x - 14/3.

There is only ONE y-coordinate at the point of intersection, so x must equal (5/3)x - 14/3 at that point.

 

[mmm4444bot]

-4 Nope.

If you had shown your work, perhaps I could see how you got -4.

 

[Belby]

(5/3)x-14/3=X
2/3-14/3=-4

 

[mmm4444bot]

(5/3)x-14/3=X

2/3-14/3=-4

Ah, I think I see the error.

When we subtract x from (5/3)x, we get (2/3)x, not 2/3.

\(\displaystyle \frac{5}{3} x - \frac{14}{3} = x\)

Subtract x from both sides.

\(\displaystyle \frac{5}{3} x - x - \frac{14}{3} = x - x\)

\(\displaystyle \left( \frac{5}{3} - \frac{3}{3} \right) x - \frac{14}{3} = 0\)

\(\displaystyle \frac{2}{3} x - \frac{14}{3} = 0\)

Now, add 14/3 to both sides.

\(\displaystyle \frac{2}{3} x + \frac{14}{3} - \frac{14}{3} = \frac{14}{3} + 0\)

\(\displaystyle \frac{2}{3} x = \frac{14}{3}\)

Multiply both sides by 3/2.

\(\displaystyle \frac{3}{2} \cdot \frac{2}{3} x = \frac{3}{2} \cdot \frac{14}{3}\)

\(\displaystyle x = 7\)

 

[Belby]

Thank you. I would have never gotten the correct answer.

 

[Denis]

(5/3)x-14/3=X
2/3-14/3=-4

Belby, you are losing your time by trying to solve stuff like intersection points if you are
unable to solve such a basic equation.
It would be way to your advantage to back up some, and make sure you understand the basics....

 

[mmm4444bot]

… I would have never gotten the correct answer.

Then this is an opportunity to learn something.

Do you now understand why A = 7 and B = 7 ?

If you're still unsure, we can certainly continue this discussion.