Another Grade 11 Trig problem

[needshelp]

Okay I have one more problem :shock: and after this I promise to leave you guys alone.

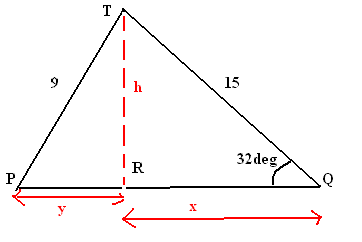
Two guy wires, 15m and 9m in length, fasten a radio tower from two point P and Q. The angle of elevation of the longer wire is 32degrees.

a) How far apart are points P and Q?
b) How tall is the tower?

I think the answer for a is susposed to be 16.9m and the answer for b is 7.9m, but I am not sure how to get those, cause I got totally different answers.

Thanks again, you guys are the best

 

[Gene]

One way is use the law of sines to find the other angle of elevation and the sum of angles in triangle for the third angle. Use the law of cosines to find the third side, (the distance from P to Q.) The height = 15sin(32)

Show your work if you want your way corrected.

 

[needshelp]

this is my work, but it doesn't work out to the right answer[/url]

 

[Unco]

G'day, Needshelp.

We have

From triangle QRT,
\(\displaystyle \L \cos{32} = \frac{adj}{hyp} = \frac{x}{15}\)
this gives us the \(\displaystyle x\) part of the base length.

\(\displaystyle \L \sin{32} = \frac{opp}{hyp} = \frac{h}{15}\)
this gives us the height, \(\displaystyle h\)

Knowing \(\displaystyle h\), we can determine \(\displaystyle y\) by Pythagoras with triangle PTR.

Can you proceed?

 

[Gene]

a) only works for right triangles. The result isn't PQ, it is PQ₁
The angle of elevation of the 15M side is <P(=32°), not <Q
so it is
sin(Q)/15 = sin(32)/9
so >Q = 62°
It looks like you are saying
<P₃ = ?
But it must be <T and it =
180-(P+Q)
Try again with those corrections.

 

[opticaltempest]

There's a mistake in solving for sin(P) in part (b). It should be (9sin(32))/15.

EDIT: Gene's post from above looks correct... Angle P should be 32 degrees.
That would make what I said above incorrect. Sorry

 

[needshelp]

wait never mind, now I am a bit confused. Do I still do that thing to find x and y?

 

[needshelp]

a) only works for right triangles. The result isn't PQ, it is PQ₁
The angle of elevation of the 15M side is <P(=32°), not <Q
so it is
sin(Q)/15 = sin(32)/9
so >Q = 62°
It looks like you are saying
<P₃ = ?
But it must be <T and it =
180-(P+Q)
Try again with those corrections.

If the angle P is 32degrees, why isn't it sin32/15?

 

[needshelp]

never mind, i figured my problem! Thanks so much

oh and for this question, does my drawing look right?

 

[Unco]

tan(52) is not equal to 60/76 so the triangle is not right-angled.

The length can certainly be determined, though. If we are to use right-angled trigonometry, there's just a bit of algebra.

We have something like this

    <-        76       ->          
              <-    x  ->
    +---------+---------+
     \        |     52 /
     
       \      |      /
                h  
     60  \    |    /   ?
           
           \  |  /
              
              *
     
   (Diagram not to scale)

We know from the right-hand triangle
\(\displaystyle \L \tan{52} = \frac{h}{x}\) [1]

and we also know from Pythagoras in the left-hand triangle
\(\displaystyle \L h^2 + (76 - x)^2 = 60^2\) [2]

Substituting \(\displaystyle h\) from [2] into [1] gives \(\displaystyle x\), etc.