Instructions: Find the area of each figure.
Problem: See attachment for diagram.
[attachment=0:wck66q9y]10-4sg-5.png[/attachment:wck66q9y]
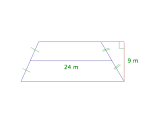
Ok so here another crazy problem, this one is a trapezoid (thanks for correcting me, Subhotosh Khan) with a line cutting through the middle of a trapezoid with 24 m and no measurements of the top or bottom of the trapezoid with a height of 9 m. I would have no clue how to do this. Any help please? :?: (note the red lines are not part of the trapezoid and congruent markings and right angle symbols are in green)
Problem: See attachment for diagram.
[attachment=0:wck66q9y]10-4sg-5.png[/attachment:wck66q9y]
Ok so here another crazy problem, this one is a trapezoid (thanks for correcting me, Subhotosh Khan) with a line cutting through the middle of a trapezoid with 24 m and no measurements of the top or bottom of the trapezoid with a height of 9 m. I would have no clue how to do this. Any help please? :?: (note the red lines are not part of the trapezoid and congruent markings and right angle symbols are in green)