PaulKraemer
New member
- Joined
- Apr 10, 2011
- Messages
- 45
Hi,
I am having trouble with the following problem:
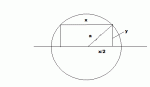
Find the dimensions of the rectangle of maximum area that can be inscribed in a semicircle of radius 'a', if two vertices lie on the diameter.
First, I determined that if I let x = the height of the rectangle, then the width of the rectangle is 2[sqrt(a^2 - x^2)]. If this is correct, the area of the rectangle would be:
A(x) = (2x)[sqrt(a^2 - x^2)]
I found the derivative of the above formula to be:
A'(x) = [x / sqrt(a^2 - x^2)] + [2(sqrt(a^2 - x^2))] = (-2x^2 + 2a^2 + x) / sqrt(a^2 - x^2)
I tried to find the zeros of the above equation by using the quadratic formula and came out with a critical number of x = [-1 - sqrt(1 + 16a^2)] / (-4)
To find out if this is a max or not, I tried taking the second derivative A' ' (x). I got a really complicated, messy equation and to have to plug [-1 - sqrt(1 + 16a^2)] / (-4) into it to perform the second derivative test seems like its more than my book would expect (this is only problem #7 in this chapter).
I think I must have gone wrong somewhere. If anyone could give me a clue, I'd really appreciate it.
Thanks,
Paul
I am having trouble with the following problem:
Find the dimensions of the rectangle of maximum area that can be inscribed in a semicircle of radius 'a', if two vertices lie on the diameter.
First, I determined that if I let x = the height of the rectangle, then the width of the rectangle is 2[sqrt(a^2 - x^2)]. If this is correct, the area of the rectangle would be:
A(x) = (2x)[sqrt(a^2 - x^2)]
I found the derivative of the above formula to be:
A'(x) = [x / sqrt(a^2 - x^2)] + [2(sqrt(a^2 - x^2))] = (-2x^2 + 2a^2 + x) / sqrt(a^2 - x^2)
I tried to find the zeros of the above equation by using the quadratic formula and came out with a critical number of x = [-1 - sqrt(1 + 16a^2)] / (-4)
To find out if this is a max or not, I tried taking the second derivative A' ' (x). I got a really complicated, messy equation and to have to plug [-1 - sqrt(1 + 16a^2)] / (-4) into it to perform the second derivative test seems like its more than my book would expect (this is only problem #7 in this chapter).
I think I must have gone wrong somewhere. If anyone could give me a clue, I'd really appreciate it.
Thanks,
Paul