angles of four panels in 3D

[slowaero]

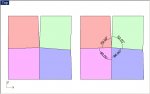
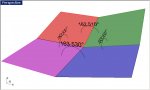
I am looking for an equation to determine the angle to rotate each of the three junctions of the panels so the gap between the green and pink closes. Like the in the perspective illustration. The perspective illustration angle is between 16 and 17 degrees arrived at by try, try, and try again. I will also need to cut another sliver out of the folded piece and fold it up again.

Thanks for you help.

SA

 

[tkhunny]

Are you sure your definition is complete and the solution unique? What can be moved? Are the far corners moving up the same amount? How do you control the movement?

 

[slowaero]

Thanks tkhunny,

I can rotate the panels at the joints between the different colors. I want to know how many degrees to rotate the joint between the red and fuchsia, then rotate the red and fuchsia as a unit on the line between the fuchsia and the blue, then rotate the red, fuchsia, and blue unit on the line between the blue and the green so that the 5 degree gap is closed.

Regards,
SA

 

[tkhunny]

I'm not quite seeing it. Maybe the "regular" demonstration will inspire someone.

Consider a circle or radius 'r'. Cut out a 5º wedge. What does it take to close this gap?

Closing the gap requires bulging of the cut circle into a right circular cone with slant height 'r' and radius '\(\displaystyle r_{1}\)' and height 'h'. The surface areas are identical, thus.

\(\displaystyle \left(1-\frac{5}{360}\right)\pi r^{2} = \pi r r_{1} \implies r_{1} = \frac{71}{72}r\)

And the height is found by the Pythagorean Theorem. \(\displaystyle h = r\sqrt{\frac{143}{5184}}\)

The official angle, \(\displaystyle \theta\), then is given by \(\displaystyle \tan(\theta) = \frac{h}{r_{1}} = \frac{\sqrt{143}}{71} \implies \theta = 9.56^{\circ}\)

This is an ideal circumstance, but your more general situation shouldn't be too far from that. Of course, you know already that it isn't too far.

 

[slowaero]

Sorry I am not better at explaining. tkhunny, The far corners do not have to move the same amount. The outer edges are arbitrary and not pertinent to my problem.

Hopefully this new illustration will help. In this illustration I rotated the three touching panels along their joining edges so that the angle between their surfaces is 163.53 degrees. I did this with trial and error. The green and red panel ended up at 162.51 degrees. I am seeking an equation that will give me an angle I can rotate the touching panels so all four panels touch and so all the panels will have that same angle in relation to their touching panels.

I will always have as a starting point the angles between four panels. In the example shown above in my first post - illustration called "four panels on flat page" the angles are 89, 92, 88, and 86.