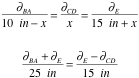Algebra Help

[ribeiro.rob]

Hello,

I'm working on this problem for a Mechanics of Material class and I'm left with three ratios equaling one another. Please see below:

x=P*1.655 E-6
y=P*2.759E-6
z=0.01

[x/(10-c)] = [y/c] = [z/(15+c)]

The solution that my professor showed me was completed based on the following "formula" if you will;

[(x+z)/(25)] = [(z-y)/15)]

Knowing this "formula" I can solve the problem but I'm unable to derive this formula myself!

Can anyone help me out?

Thanks taking the time to read this post and I look forward to replys!

Rob

 

[mmm4444bot]

Can anyone help me out?

I don't know what you've been asked to do. I'm not sure what you specifically want help with.

Are you trying to solve the following system of two equation for P and c ?

(0.000001655 P)/(10 - c) = (0.000002759 P)/c

(0.000002759 P)/c = 0.01/(15 + c)

If so, then I can show you how to get the following values (rounded).

P = 1066.0981

c = 6.2506

 

[ribeiro.rob]

First of all thanks for looking at this problem! Greatly appreciated!

What I'm trying to figure out is how the following relationship is derived:

d[sub:2dlh3qnt]ba[/sub:2dlh3qnt]+d[sub:2dlh3qnt]e[/sub:2dlh3qnt]/25=d[sub:2dlh3qnt]e[/sub:2dlh3qnt]-d[sub:2dlh3qnt]cd[/sub:2dlh3qnt]/15

from:

d[sub:2dlh3qnt]ba[/sub:2dlh3qnt]/10-x=d[sub:2dlh3qnt]cd[/sub:2dlh3qnt]/x=d[sub:2dlh3qnt]e[/sub:2dlh3qnt]/15+x

I have attached a pdf of my complete solution to this problem for addition clarification if required. I have solved the problem 2 ways as of step three (one of which is the way the problem was solved on the original reply).

 

[mmm4444bot]

What I'm trying to figure out is how the following relationship is derived:

(d[sub:3eylz2po]ba[/sub:3eylz2po]+ d[sub:3eylz2po]e[/sub:3eylz2po])/25 = (d[sub:3eylz2po]e[/sub:3eylz2po]- d[sub:3eylz2po]cd[/sub:3eylz2po])/15

from:

d[sub:3eylz2po]ba[/sub:3eylz2po]/(10 - x) = d[sub:3eylz2po]cd[/sub:3eylz2po]/x = d[sub:3eylz2po]e[/sub:3eylz2po]/(15 + x)

We need to include the red grouping symbols above, when typing ratios where numerators or denominators are algebraic expressions.

I'm thinking that we can change the latter proportion into the former through some combination of substitution and simplification. Let me play with it for a few minutes.

 

[mmm4444bot]

Okay — I figured out one way.

Step 1: Solve the following equation for x

\(\displaystyle \frac{\partial_{BA}}{10 - x} \;=\; \frac{\partial_E}{15 + x}\)

Step 2: Substitute the result for x into the following expression, and simplify

\(\displaystyle \frac{\partial_{BA}}{10 - x}\)

Step 3: Solve the following equation for x

\(\displaystyle \frac{c}{x} \;=\; \frac{\partial_E}{15 + x}\)

Step 4: Substitute the result for x into the following expression, and simplify

\(\displaystyle \frac{\partial_E}{15 + x}\)

The results from steps 2 and 4 are equal (Transitive Property of Equality)

Let me know, if you cannot reproduce this; I was starting to get confused transcribing my notes (with your x,y,z substitutions, and my own b,c,e substitutions, resulting in double-use of both x and c), so I might have goofed this post.

Cheers ~ Mark