If I have an equation like this
\(\displaystyle [2f+(p+q) ]*[2f-(p+q) ]=4pq\)
Are any of the three methods below any better than the other for creating factors of \(\displaystyle 4pq\)?
Are any of them incorrect?
Is there a 'correct' way that should always be used?
Many thanks

Method 1.
\(\displaystyle [2f+(p+q) ]*[2f-(p+q) ]=4pq\)
\(\displaystyle let\ \ \ 4pq=rs\)
\(\displaystyle 2f+(p+q)=r\)
\(\displaystyle 2f-(p+q)=s\)
\(\displaystyle 4f=r+s\ \ \ \ \ \ \ \ \ \ \ \ \ f=\dfrac{r+s}{4}\)
\(\displaystyle 2(p+q)=r-s\ \ \ \ \ \ \ \ p+q=\dfrac{r-s}{2}\)

Method 2.
\(\displaystyle [2f+(p+q) ]*[2f-(p+q) ]=4pq\)

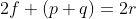
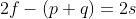



Method 3.
\(\displaystyle [2f+(p+q) ]*[2f-(p+q) ]=4pq\)

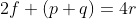
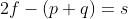


\(\displaystyle [2f+(p+q) ]*[2f-(p+q) ]=4pq\)
Are any of the three methods below any better than the other for creating factors of \(\displaystyle 4pq\)?
Are any of them incorrect?
Is there a 'correct' way that should always be used?
Many thanks
Method 1.
\(\displaystyle [2f+(p+q) ]*[2f-(p+q) ]=4pq\)
\(\displaystyle let\ \ \ 4pq=rs\)
\(\displaystyle 2f+(p+q)=r\)
\(\displaystyle 2f-(p+q)=s\)
\(\displaystyle 4f=r+s\ \ \ \ \ \ \ \ \ \ \ \ \ f=\dfrac{r+s}{4}\)
\(\displaystyle 2(p+q)=r-s\ \ \ \ \ \ \ \ p+q=\dfrac{r-s}{2}\)
Method 2.
\(\displaystyle [2f+(p+q) ]*[2f-(p+q) ]=4pq\)
Method 3.
\(\displaystyle [2f+(p+q) ]*[2f-(p+q) ]=4pq\)
