JanelSalas
New member
- Joined
- Nov 9, 2015
- Messages
- 1
Please make your proofs concise.
1. If a<b, then a< (a+b)/2 < b
2. If I and J are open intervals, prove that either
3. Let x1, x2
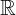 . If x1 is not equal to x2, then there exists ε1>0 and ε2>0 such that N(x1, ε1)
. If x1 is not equal to x2, then there exists ε1>0 and ε2>0 such that N(x1, ε1)
4. Let β be a lower bound for E
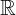 . Then β = inf E if and only if for every ε>0, there exists x
. Then β = inf E if and only if for every ε>0, there exists x
5. Let E be a bounded set. If F
PLEASE HELP ME TO PROVE THIS. :?
1. If a<b, then a< (a+b)/2 < b
2. If I and J are open intervals, prove that either
I∩ J =Ø orI∩ J
is also an open interval 3. Let x1, x2
∈
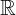
∩
N( x2, ε2) =Ø
4. Let β be a lower bound for E
⊂
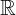
∈
E such that x <β +ε5. Let E be a bounded set. If F
⊂
E, then F is also bounded. Furthermore, sup F≤
sup E and inf E≤
inf FPLEASE HELP ME TO PROVE THIS. :?
