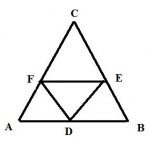
In the diagram attached: triangleABC is an equilateral and D,E,F are the midpoints of its sides.
Express each sum as a single vector.
Here is what I got, but I don't think it's right.
a) AF + DB = FD
b) DE + DB = EB
c) FA + EB = AD
d) DA + EC = AF
e) AF + DE = 0
Could someone please help me clarify?
I very much appreciate all help :shock:
Express each sum as a single vector.
Here is what I got, but I don't think it's right.
a) AF + DB = FD
b) DE + DB = EB
c) FA + EB = AD
d) DA + EC = AF
e) AF + DE = 0
Could someone please help me clarify?
I very much appreciate all help :shock: