The question says:
Find the absolute extreme of each function given the interval. The extremes (extrema) are just the minimum and maximum values of f(x) within the given interval.
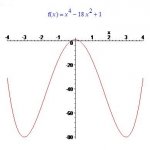
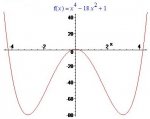
We are supposed to use the extreme value theorem The extreme value theorem says that if f(x) is real and continuous in the bounded interval, then both a minimum f(x) and a maximum f(x) for that interval exist. So is f(x) = x[sup:3uj8xgbk]4[/sup:3uj8xgbk] - 18x[sup:3uj8xgbk]2[/sup:3uj8xgbk] + 1 real and continuous over the interval [-4, 4]? If it is, the problem is soluble, at least in principle.
The [-4,4} are the intervals.
The instructor has told me to solve for 0 but my problem is I can't seem to do it correctly. He says I need to find f'(x) first and I think I keep messing that up.
so if I have f(x) = x^4 - 18x^2 + 1
I thought I would do:
f ' (x) = 4x^3 - 36 This is an error. What is the derivative of - 18x[sup:3uj8xgbk]2[/sup:3uj8xgbk]?
I need to come up with the absolute minimum and absolute maximum.