A Trig Application (maximum water volume in gutter)

[ty2391]

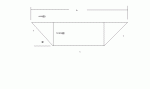
I have this question to do for my next class:

A gutter is to be made from a metal sheet of width 3 metres by bending up one third of the sheet on each side through an angle ?. How should the ? be chosen so that the gutter will carry the maximum amount of water?

This is what I pictured it to be:

However, after that, I can't figure out where to start.

Could someone help me out? A full solution would be very much appreciated.

 

[Loren]

Re: A Trig Application

If I were solving this, I would draw the perpendiculars from the vertex of each of the base angles. This would give me right triangles. Theta becomes 90° + an acute angle (call it anything you want) and I could then consider the area of the right triangle and how it becomes a maximum in terms this new acute angle. The middle rectangle remains constant. The two right triangles are congruent.

 

[galactus]

Re: A Trig Application

Let's do it this way. You have the angle on the inside of the gutter. I will put it on the outside. Then just subtract from 180 to get the inside angle you have.

The area of the trapezoid is given by \(\displaystyle A=\frac{1}{2}h(1+b)\)...............[1]

But, \(\displaystyle h=sin{\theta}, \;\ and \;\ b=1+2cos{\theta}\)

Sub them into [1]:

\(\displaystyle A=\frac{1}{2}sin{\theta}(2+2cos{\theta})=sin{\theta}(1+cos{\theta}), \;\ 0\leq{\theta}\leq\frac{\pi}{2}\)

Now, this is what must be minimized. Let us know what you get.

 

[ty2391]

Thank so much for your help! So, after the last step you wrote, I expanded it to become sin? + sin?cos?. I then took the derivative of that, so:
dA/d? = cos? + cos²? - sin²?. To maximize the area of the trapezoid, dA/d? = 0. Then solve for ?, and I got ? = pi/3, or 60 degrees.

 

[galactus]

That's very good and correct. So, remember to subtract that amount form 180 for your angle.