a simple limit question

[serenaleesl]

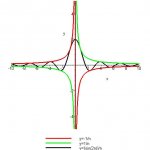
how do u find the limit of sin(2n) / n at infinity without converting sin(2n) to 2sin(n)cos(n)?

I thought of .. Lim (n-> infinity) [1/n x sin (2n) ] = 0 since 1/n goes to 0 when n=infinity and sin(2n) diverges when n is infinity..is this method wrong?

 

[BigGlenntheHeavy]

Try the old squeeze play.

\(\displaystyle -1 \ \le \ sin(2n) \ \le \ 1, \ \frac{-1}{n} \ \le \ \frac{sin(2n)}{n} \ \le \frac{1}{n}.\)

\(\displaystyle \lim_{n\to\infty}\frac{-1}{n} \ \le \ \lim_{n\to\infty}\frac{sin(2n)}{n} \ \le \ \lim_{n\to\infty}\frac{1}{n}.\)

\(\displaystyle 0 \ \le \ \lim_{n\to\infty}\frac{sin(2n)}{n} \ \le \ 0.\)

\(\displaystyle Ergo, \ \lim_{n\to\infty}\frac{sin(2n)}{n} \ = \ 0, \ its \ only \ choice.\)

See graph below for visual enhancement. Observe how [sin(2n)]/n is "squeeze" between the other two .

[attachment=0:32c4dykr]http://www.jpg[/attachment:32c4dykr]