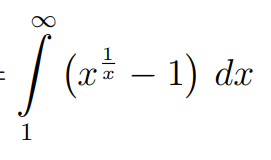king of pasta
New member
- Joined
- Mar 13, 2023
- Messages
- 3
At first glance, both of them appeared to me as diverging but my university professor said(as a side note after class) that both of them undoubtedly converging
I will be glad if u can explain to me how and why?
n=1∑∞(arctan(n+sin(n)1))2∫1∞(xx1−1)dx
∫1∞(xx1−1)dx(adding the relevent integral as a jpeg)
I will be glad if u can explain to me how and why?
n=1∑∞(arctan(n+sin(n)1))2∫1∞(xx1−1)dx
∫1∞(xx1−1)dx(adding the relevent integral as a jpeg)