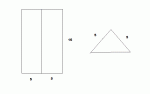
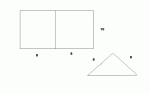
A problem: using 10-by-16-ft tarp to form pup tent
- Thread starter watever
- Start date
Re: A problem
I suppose it depends on how high you pitch your tent. Let's assume the inside corners will have angle of 45 degrees.
The volume if it were folded along the long seam (16 feet) as in drawing [1], then we would have \(\displaystyle V=5cos(\frac{\pi}{4})5sin(\frac{\pi}{4})16=200\)
Suppose now it was folded the pother way as in drawing [2]; \(\displaystyle 8cos({\frac{\pi}{4})8sin(\frac{\pi}{4})10=320\)
Well, there is one case where it makes a difference.
I suppose it depends on how high you pitch your tent. Let's assume the inside corners will have angle of 45 degrees.
The volume if it were folded along the long seam (16 feet) as in drawing [1], then we would have \(\displaystyle V=5cos(\frac{\pi}{4})5sin(\frac{\pi}{4})16=200\)
Suppose now it was folded the pother way as in drawing [2]; \(\displaystyle 8cos({\frac{\pi}{4})8sin(\frac{\pi}{4})10=320\)
Well, there is one case where it makes a difference.
Attachments
Re: A problem
Okey-doke then. If we set up the volume in terms of theta, then we can differentiate to find the angle that maximizes the volume. As I previously stated, it is 45 degrees. But here we show it.
\(\displaystyle \frac{d}{d{\theta}}[400cos{\theta}sin{\theta}]=800cos^{2}{\theta}-400=400cos(2{\theta})\)
\(\displaystyle cos(2\theta)=0\)
\(\displaystyle {\theta}=\frac{\pi}{4}\)
Proceed as before.
Okey-doke then. If we set up the volume in terms of theta, then we can differentiate to find the angle that maximizes the volume. As I previously stated, it is 45 degrees. But here we show it.
\(\displaystyle \frac{d}{d{\theta}}[400cos{\theta}sin{\theta}]=800cos^{2}{\theta}-400=400cos(2{\theta})\)
\(\displaystyle cos(2\theta)=0\)
\(\displaystyle {\theta}=\frac{\pi}{4}\)
Proceed as before.
Is this another approach?
The volume of the tent = area of the triangular cross-section times the length.
The area of the cross section = (1/2)hbl where h is the height, b is the base and l is the length. The width of the tarp will be called w. Using Pythagorean Thm, \(\displaystyle (\frac{b}{2})^2 = (\frac{w}{2})^2-h^2\)
\(\displaystyle b^2=4(\frac{w^2}{4}-h^2)\)
\(\displaystyle b^2=w^2-4h^2\)
\(\displaystyle b=\pm\sqrt{w^2-4h^2}\)
\(\displaystyle V=\frac{1}{2}bhl=\frac{1}{2}hl\sqrt{w^2-4h^2}\)
Now we could substitute in w=10 and l=16 for case 1 and differentiate to determine maximum volume. Then for case 2 substitute in w=16 and l=10 and differentiate to determine maximum volume. Then we compare those results.
Possible or not???
The volume of the tent = area of the triangular cross-section times the length.
The area of the cross section = (1/2)hbl where h is the height, b is the base and l is the length. The width of the tarp will be called w. Using Pythagorean Thm, \(\displaystyle (\frac{b}{2})^2 = (\frac{w}{2})^2-h^2\)
\(\displaystyle b^2=4(\frac{w^2}{4}-h^2)\)
\(\displaystyle b^2=w^2-4h^2\)
\(\displaystyle b=\pm\sqrt{w^2-4h^2}\)
\(\displaystyle V=\frac{1}{2}bhl=\frac{1}{2}hl\sqrt{w^2-4h^2}\)
Now we could substitute in w=10 and l=16 for case 1 and differentiate to determine maximum volume. Then for case 2 substitute in w=16 and l=10 and differentiate to determine maximum volume. Then we compare those results.
Possible or not???
D
Deleted member 4993
Guest
Loren said:
Your approach and Galactus's approach are equivalent - just replace h by 8sin(T) - in the expression derived by him.
However - differentiation with respect to 'T' is easier in this case - than trying to handle sqrt and sqr terms in the expression derived by you.
skeeter
Elite Member
- Joined
- Dec 15, 2005
- Messages
- 3,216
fold the 16ft side in half ...
\(\displaystyle V = 10 \cdot \frac{1}{2} \cdot 8^2 \sin{\theta}\)
where \(\displaystyle \theta\) is the fold angle.
fold the 10ft side in half ...
\(\displaystyle V = 16 \cdot \frac{1}{2} \cdot 5^2 \sin{\theta}\)
easy to see that the max for both will occur when \(\displaystyle \theta = 90^{\circ}\)
\(\displaystyle V = 10 \cdot \frac{1}{2} \cdot 8^2 \sin{\theta}\)
where \(\displaystyle \theta\) is the fold angle.
fold the 10ft side in half ...
\(\displaystyle V = 16 \cdot \frac{1}{2} \cdot 5^2 \sin{\theta}\)
easy to see that the max for both will occur when \(\displaystyle \theta = 90^{\circ}\)