A prime counting function I have never seen
- Thread starter binbots
- Start date
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,598
Which last term?
The e^(1/ln(x)).
Here are some numbers to see how well it works and I bit of history behind how this came about. I included li(x), my equation, my equation with + and - .1 added to the e just to show that it should be e, x/ln(x)-1 and x/ln(x)
Here is what li(x) (green), my equation (red) and x/ln(x) (blue) look like on a graph on the low end as it seems to be the initial conditions as to why it works so well.
As for how I came up with this. It is believed that the prime number theorem tends to x/ln(x)-1. But it doesn’t start at -1 so I made that a variable instead x/ln(x)-y. Then knowing that y needs to get smaller as x gets larger I knew I had to combine it with ln(x) some how. Then realizing that it had to get smaller I made it the reciprocal of ln(x). Eventually it turned into
x/ln(x)-y^(z/ln(x). Then it was just days of playing around with these numbers to find what works best. I never thought it would be e at first as the base cause it seemed way to high so I had things like x/ln(x)-1.47^(13.33/ln(x)-1). I found many that worked great but eventually they would all go over li(x). Then one day I just tried e as the base and left the numerator in the exponent as 1 which is always my starting point and it worked better than all my previous ones.
As for the significance of this I think this may give some tremendous insight into the distribution of primes. It is so simple that I figured there is no way this hasn’t been discovered yet. But I can’t find anything.
Here is what li(x) (green), my equation (red) and x/ln(x) (blue) look like on a graph on the low end as it seems to be the initial conditions as to why it works so well.
As for how I came up with this. It is believed that the prime number theorem tends to x/ln(x)-1. But it doesn’t start at -1 so I made that a variable instead x/ln(x)-y. Then knowing that y needs to get smaller as x gets larger I knew I had to combine it with ln(x) some how. Then realizing that it had to get smaller I made it the reciprocal of ln(x). Eventually it turned into
x/ln(x)-y^(z/ln(x). Then it was just days of playing around with these numbers to find what works best. I never thought it would be e at first as the base cause it seemed way to high so I had things like x/ln(x)-1.47^(13.33/ln(x)-1). I found many that worked great but eventually they would all go over li(x). Then one day I just tried e as the base and left the numerator in the exponent as 1 which is always my starting point and it worked better than all my previous ones.
As for the significance of this I think this may give some tremendous insight into the distribution of primes. It is so simple that I figured there is no way this hasn’t been discovered yet. But I can’t find anything.
logistic_guy
Full Member
- Joined
- Apr 17, 2024
- Messages
- 789
This function does not exist in all mathematics books!
Are you saying that you were playing around with the original function and you invented this function by coincidence? And your new function is now working better than the original function!
Are you saying that you were playing around with the original function and you invented this function by coincidence? And your new function is now working better than the original function!
The absolute differences between [imath] \pi(x) [/imath] and any approximation function [imath] f(x) [/imath] diverge. So we consider the rate of convergence of [imath] \dfrac{\pi(x)}{f(x)}\stackrel{x\to \infty }{\longrightarrow }1. [/imath] This leads us to
[math]\begin{array}{lll} \dfrac{\pi(x)}{\dfrac{x}{\log x}}-\dfrac{\pi(x)}{\dfrac{x}{(\log x)-e^{1/ \log x} }}&=\dfrac{\pi(x)\log(x)}{x}-\dfrac{\pi(x)\log(x)-\pi(x)e^{1/ \log x}}{x}=\dfrac{\pi(x)}{x}\cdot e^{1/ \log x} \end{array}[/math]and
[math]\begin{array}{lll} e^{1/ \log x}&=1+\dfrac{1}{\log(x)}+\dfrac{1}{2\log^2(x)}+\dfrac{1}{6\log^3(x)}+\ldots\\ \end{array}[/math]
We know from Chebyshev (1851) that the error is lower than [imath] 1.1056 [/imath] and from Sylvester (1892) that the error is lower than [imath] 1.04423 [/imath] which means if we compare this value with [imath] e^{1/ \log x} [/imath] then [imath] x>10^{10}. [/imath] The given approximation is therefore only valid for very large numbers with at least ten digits. However,
[math] \left|\dfrac{\pi(10^{10})}{\operatorname{Li(10^{10})}}-1\right| <0.0002\quad\text{ whereas }\quad e^{1/\log(x)}-1<0.0444 [/math]
I think that someone made up this formula since long existing approximations have already been better.
[math]\begin{array}{lll} \dfrac{\pi(x)}{\dfrac{x}{\log x}}-\dfrac{\pi(x)}{\dfrac{x}{(\log x)-e^{1/ \log x} }}&=\dfrac{\pi(x)\log(x)}{x}-\dfrac{\pi(x)\log(x)-\pi(x)e^{1/ \log x}}{x}=\dfrac{\pi(x)}{x}\cdot e^{1/ \log x} \end{array}[/math]and
[math]\begin{array}{lll} e^{1/ \log x}&=1+\dfrac{1}{\log(x)}+\dfrac{1}{2\log^2(x)}+\dfrac{1}{6\log^3(x)}+\ldots\\ \end{array}[/math]
We know from Chebyshev (1851) that the error is lower than [imath] 1.1056 [/imath] and from Sylvester (1892) that the error is lower than [imath] 1.04423 [/imath] which means if we compare this value with [imath] e^{1/ \log x} [/imath] then [imath] x>10^{10}. [/imath] The given approximation is therefore only valid for very large numbers with at least ten digits. However,
[math] \left|\dfrac{\pi(10^{10})}{\operatorname{Li(10^{10})}}-1\right| <0.0002\quad\text{ whereas }\quad e^{1/\log(x)}-1<0.0444 [/math]
I think that someone made up this formula since long existing approximations have already been better.
Yup. Well I wouldn’t say by complete coincidence. It took about 15 years of work. But I do use a lot of trial and error to move forward. So a coincidence in general yes. Unfortunately I don’t have the expertise to investigate much further. I do have a vid on YouTube that shows the process of how I found it.
I agree there are better approximations. But this equation may shed light on why the error of x/ln(x). Unlike those other ones you talk about e^(1/ln(x) isn’t a constant and gets smaller the bigger x gets. Therefore it doesn’t diverge as it is bound to ln(x). It may not be the best but still worth investigating. Especially considering how simple it is.
Last edited:
logistic_guy
Full Member
- Joined
- Apr 17, 2024
- Messages
- 789
15 years
Have you made any publications? Were your 15 years of work proved by the mathematicians community? I am expecting that 400 pages will suffice!
I think that I will watch your video in other time as my brain is very exhausted today.
Last edited:
Any monotone decreasing function [imath] f(x) [/imath] with [imath] \displaystyle{\lim_{x \to \infty}}f(x)=1 [/imath] will do, especially if we accept that such a function only has to be valid for large [imath] x [/imath] like yours.
Prime number density is classically measured by [imath] \left|\dfrac{\pi(x)}{x}\right| < \dfrac{1}{\log(x) -c}[/imath] and you are considering [imath] \dfrac{\pi(x)}{x}\cdot e^{1/ \log(x)} .[/imath] That's not really a difference as long as you cannot show how you arrived at that function.
Prime number density is classically measured by [imath] \left|\dfrac{\pi(x)}{x}\right| < \dfrac{1}{\log(x) -c}[/imath] and you are considering [imath] \dfrac{\pi(x)}{x}\cdot e^{1/ \log(x)} .[/imath] That's not really a difference as long as you cannot show how you arrived at that function.
Last edited:
Oh ok then. Thank you for your feedback.
Don’t bother. Obviously I am not smart enough to someone like you. Sorry for wasting your time.15 years
Have you made any publications? Were your 15 years of work proved by the mathematicians community? I am expecting that 400 pages will suffice!
I think that I will watch your video in other time as my brain is very exhausted today.
Here is another thought. Chebyshev has proven that there are positive constants [imath] C_1,C_2 [/imath] such that [math] \dfrac{C_1}{\log(x)}<\dfrac{\pi(x)}{x}<\dfrac{C_2}{\log(x)} .[/math]
If I made no mistakes in my calculations then replacing [imath] \dfrac{\pi(x)}{(x)} [/imath] by [imath] \dfrac{1}{\log(x)-e^{1/\log(x)}} [/imath] results in
[math] \underbrace{\left(1-\frac{1}{C_1}\right)\log(x) }_{=K_1} < e^{1/ \log(x) } < \underbrace{\left(1-\frac{1}{C_2}\right)\log(x)}_{=K_2} [/math]
Rosser (1962) has shown that we can choose [imath] K_1=1/2 [/imath] and [imath] K_2=3/2 [/imath] for [imath] x\geq 67. [/imath] The function [imath] e^{1/\log(x)} [/imath] fulfills this condition. The equation can also be written as
[math] 1-\dfrac{1}{C_1}<\underbrace{\dfrac{e^{1/\log(x)}}{\log(x)}}_{=f(x)}< 1-\dfrac{1}{C_2}[/math]
or
[math] C_1<\dfrac{1}{1-f(x)}<C_2 [/math]
Hence, if you can prove your formula, you will directly get a relation to Chebyshev's constants and possibly improve them.
However, [imath] \displaystyle{\lim_{x \to \infty}f(x)=0} [/imath] means [imath] C_1<1<C_2 [/imath] for large enough [imath] x [/imath] which isn't any new information.
If I made no mistakes in my calculations then replacing [imath] \dfrac{\pi(x)}{(x)} [/imath] by [imath] \dfrac{1}{\log(x)-e^{1/\log(x)}} [/imath] results in
[math] \underbrace{\left(1-\frac{1}{C_1}\right)\log(x) }_{=K_1} < e^{1/ \log(x) } < \underbrace{\left(1-\frac{1}{C_2}\right)\log(x)}_{=K_2} [/math]
Rosser (1962) has shown that we can choose [imath] K_1=1/2 [/imath] and [imath] K_2=3/2 [/imath] for [imath] x\geq 67. [/imath] The function [imath] e^{1/\log(x)} [/imath] fulfills this condition. The equation can also be written as
[math] 1-\dfrac{1}{C_1}<\underbrace{\dfrac{e^{1/\log(x)}}{\log(x)}}_{=f(x)}< 1-\dfrac{1}{C_2}[/math]
or
[math] C_1<\dfrac{1}{1-f(x)}<C_2 [/math]
Hence, if you can prove your formula, you will directly get a relation to Chebyshev's constants and possibly improve them.
However, [imath] \displaystyle{\lim_{x \to \infty}f(x)=0} [/imath] means [imath] C_1<1<C_2 [/imath] for large enough [imath] x [/imath] which isn't any new information.
logistic_guy
Full Member
- Joined
- Apr 17, 2024
- Messages
- 789
No one is smarter than others. It's only that different people have different interests.
I watched your video and I think that it's worth exploring. I also watched the other videos about prime numbers and golden ratio. They are interesting. I hope that you explore more in what you got so far to achieve your ultimate potential in that function.
Fifteen years sound a lot, but to be honest it's nothing compared to those people who spent their life time to improve something. Many of them did not get the expected result they wanted, but they have learnt a lot of things along the way. Someone else would probably continue their work and this is a proof that their long-term effort is worth everything.
If someone constructively criticize you, you should be happy, not mad. Without this constructive criticism, you can develop, but slowly. Therefore, make the most of everything positive said about your work.
I am sorry for yesterday if I accidentally said anything that may have hurt you. It was just that I solved 30 problems and my brain was not functioning properly to watch a video.
Just want to say that you have a nice playlist over there, and I am a fan of Careless Whisper by George Michael
I forgot to mention that some theorems about the prime number density require the Riemann hypothesis to hold and I'm not certain whether Rosser's result does or does not. You can find a short description and some links about the relationship between [imath] \pi(x) [/imath] and the Riemann hypothesis here:
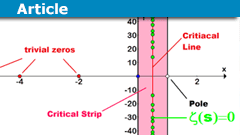
www.physicsforums.com
The History and Importance of the Riemann Hypothesis
The history of the Riemann hypothesis may be considered to start with the first mention of prime numbers in the Rhind Mathematical Papyrus around 1550 BC.
www.physicsforums.com
Thank you for this information. Been investigating all morning. To me it just seems like too much of a coincidence that it contains e and 1 to not mean something. I tried so many versions of y^(z/ln(x) and they all eventually would go over li(x). Plus li(x) does go above and below the actual value an infinite amount of times. Maybe mine stays consistently below.
As for proving my formula that may be rather difficult. I wouldn’t even know where to begin. I just play around with primes as a hobby. That is why I’m asking for help. You guys are magicians to me. I’m just a weirdo who spends hours on end playing on a calculator.
Thanks for this. First off it was my mistake to say work as this is my hobby. Not career. As you can probably tell from my vids I just play around and sometimes stumble across something interesting. Unfortunately it usually takes me awhile to figure out how I found it if I find it at all. But this formula does seem to be special. I’m just throwing it out there and hoping someone can do something with it.No one is smarter than others. It's only that different people have different interests.
I watched your video and I think that it's worth exploring. I also watched the other videos about prime numbers and golden ratio. They are interesting. I hope that you explore more in what you got so far to achieve your ultimate potential in that function.
Fifteen years sound a lot, but to be honest it's nothing compared to those people who spent their life time to improve something. Many of them did not get the expected result they wanted, but they have learnt a lot of things along the way. Someone else would probably continue their work and this is a proof that their long-term effort is worth everything.
If someone constructively criticize you, you should be happy, not mad. Without this constructive criticism, you can develop, but slowly. Therefore, make the most of everything positive said about your work.
I am sorry for yesterday if I accidentally said anything that may have hurt you. It was just that I solved 30 problems and my brain was not functioning properly to watch a video.
Just want to say that you have a nice playlist over there, and I am a fan of Careless Whisper by George Michael
Thanks for the compliment on my vids. I was pretty upset that the golden ratio didn’t work out. But it did lead to the basis of this latest formula.
Why the careless whisper reference? Did I have it playing in the background ground of one of my vids? lol
Oh I am well aware of the Riemann hypothesis. It drives me nuts as I can’t deal with anything too abstract. Hence my problem with advanced mathematics. It doesn’t stop me from trying though.I forgot to mention that some theorems about the prime number density require the Riemann hypothesis to hold and I'm not certain whether Rosser's result does or does not. You can find a short description and some links about the relationship between [imath] \pi(x) [/imath] and the Riemann hypothesis here:
The History and Importance of the Riemann Hypothesis
The history of the Riemann hypothesis may be considered to start with the first mention of prime numbers in the Rhind Mathematical Papyrus around 1550 BC.