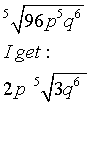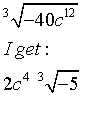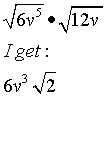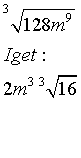You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
A little help?
- Thread starter WTF?
- Start date
Absolutely correct.WTF? said:I have a little problem to simplify that I'm a bit confused about,
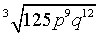
I try it, and I get this:
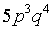
Both of those are the same, yes.WTF? said:I also have this one that's confusing as well:
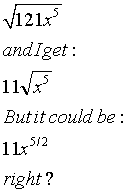
zerodegrees
New member
- Joined
- Feb 8, 2006
- Messages
- 24
Remember, roots are still exponents.
They are instead FRACTIONAL POWERS.
So...a square root would be RAISED TO THE ONE-HALF POWER.
A cube root would be RAISED TO THE ONE-THIRD POWER.
Hope this helps.
They are instead FRACTIONAL POWERS.
So...a square root would be RAISED TO THE ONE-HALF POWER.
A cube root would be RAISED TO THE ONE-THIRD POWER.
Hope this helps.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,978
I did not mean to imply that!WTF? said:Hmm...the other two are right?
I expected you to study and see if they are correct.
Ah, ok.pka said:I did not mean to imply that!WTF? said:Hmm...the other two are right?
I expected you to study and see if they are correct.
But I still don't know how you got the first two. :x Why is there two q's?
But when I try a value, it seems to work. :x
Eva Barragan
New member
- Joined
- Feb 8, 2006
- Messages
- 44
Mr. Danielzyck?
pka said:Do you see how it works?
:?
The book doesn't say that, it just leaves the power as is if it doesn't divide by the root evenly. :?:
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,978
It is a sorry state of mathematical notation!
The ‘root’ notation is the most confused!
Many who write about this have no clear idea themselves what it means
All I can say is “Go with your book or your instructor.”
Know that either may be incorrect!
The ‘root’ notation is the most confused!
Many who write about this have no clear idea themselves what it means
All I can say is “Go with your book or your instructor.”
Know that either may be incorrect!
pka said:It is a sorry state of mathematical notation!
The ‘root’ notation is the most confused!
Many who write about this have no clear idea themselves what it means
All I can say is “Go with your book or your instructor.”
Know that either may be incorrect!
I tried substituting a value into yours and I got two distinct answers though. :?:
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,978
You must have made mistakes in the way you calculated!WTF? said:I tried substituting a value into yours and I got two distinct answers though. :?:
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,978
I began working on this problem in 1964.
I have given many talks and workshops to/for in-service teachers.
I can tell you that I have had the most trouble with radicals.
It is so simple I think: the nth root of k is a number such that the nth power is k.
That is if \(\displaystyle \L
\sqrt[n]{b} = c\quad \Rightarrow \quad \left( c \right)^n = b\) .
Therefore, \(\displaystyle \L
\sqrt[n]{{x^m }}\quad \Rightarrow \quad \left( {x^m } \right)^{1/n} \quad \Rightarrow \quad x^{m/n}\) .
\(\displaystyle \L
\frac{{10}}{3} = 3 + \frac{1}{3}\) so that \(\displaystyle \L
\sqrt[3]{{x^{10} }} = 3\sqrt[3]{x}\) .
But we must be very careful a domain issuers.
Look at this \(\displaystyle \L
\sqrt[4]{{x^8 y^6 }} = x^2 |y|\sqrt {|y|}\) .
You must see that the absolute value insures the proper domain
I have given many talks and workshops to/for in-service teachers.
I can tell you that I have had the most trouble with radicals.
It is so simple I think: the nth root of k is a number such that the nth power is k.
That is if \(\displaystyle \L
\sqrt[n]{b} = c\quad \Rightarrow \quad \left( c \right)^n = b\) .
Therefore, \(\displaystyle \L
\sqrt[n]{{x^m }}\quad \Rightarrow \quad \left( {x^m } \right)^{1/n} \quad \Rightarrow \quad x^{m/n}\) .
\(\displaystyle \L
\frac{{10}}{3} = 3 + \frac{1}{3}\) so that \(\displaystyle \L
\sqrt[3]{{x^{10} }} = 3\sqrt[3]{x}\) .
But we must be very careful a domain issuers.
Look at this \(\displaystyle \L
\sqrt[4]{{x^8 y^6 }} = x^2 |y|\sqrt {|y|}\) .
You must see that the absolute value insures the proper domain