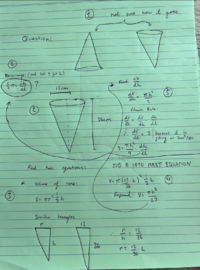
The question is:
A 36 cm high cone with a base of radius 12cm is filled with water at a constant rate of 3 cm^3 /sec. What is the rate of change of height in cm/sec when the water in the cone has a depth of 9cm?
Any help would be greatly appreciated

Hi Lucas,
I am far from an expert on this subject, since I am also currently learning rates of change and also posting questions upon it. But I'm sure I could grasp this question, but I think my answer would have to be checked and corroborated by one of the resident members.
Basically you are looking for dh/dt, which is the rate of change of height per sec. You can get this by following the formula
dh/dt = dV/dt divided by dV/dh
dV/dt is the rate of change of the volume per sec, which if you read the question carefully you'll notice that you already have this, it is 3 cm^2/sec (because it gives you information in volume cm^3 and time in sec). So
dV/dt = 3
Next you need to find dV/dh, which is the derivative of the function V = f(h). But since the formula for the volume for a cone of (1/3)pi * r^2 * h is in terms of r and h, you'll need to change that r to its equivalent in h to properly keep the function in respect of h (it's like having y = 2x + z and you don't want the z there, in this case we don't want the r) so using trig to find the r in terms of h, and using the angle theta that separates the height and the slant height of the cone...
tan theta = r/h
tan theta = 12/36
tan theta = 1/3
1/3 = r/h
h * 1/3 = r
r = h/3
So replace the r in the formula for the volume of a cone with h/3 and you now have V = (pi*h^3)/27. Since you now have your V = f(h) you can get the derivative dV/dh = (pi*h^2)/9.
So now you can use dV/dt divided by dV/dh and you get
dh/dt = 27/(pi*h^2)
This is used to find the rate of change of height over time, and since you want to know the rate of change when the height is 9cm, punch this into dh/dt
dh/dt = 27/(pi*9^2) = 27/(pi * 27) = 1/pi cm/sec, or 0.318 cm/sec
This would seem a lot easier if you write the equations on paper and thus in a better format.