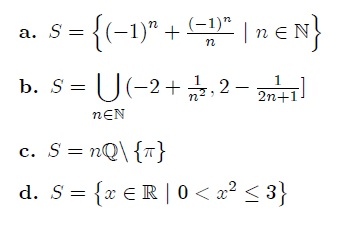
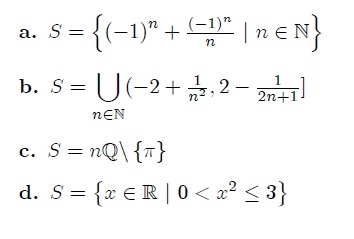
Find the interior int (S), the boundary bd (S), the closure cl (S), and the set accumulation points S' of each subset S of R.
Classify the set S as open, closed, neither, or both. Is S a compact set? Justify your answers.
For each subset S of R, fi…nd its supremum sup S, maximum max S, infi…mum inf S, and minimum min S, if exists. Otherwise, write "DNE". Justify your answers.
a. S = { (-1)^n + (-1)^n/n | n is an element of N }
b. S = U [ -2+1/(n^2), 2-1(2n+1) ] when n is an element of N
c. S = nQ \ {pi}
d. S = { x is an element of R | 0 < x^2 <= 3 }
please answer any of the following questions, if not all.
