3-D vector problem: "A 3-D box has the dimensions 6, 8 and 4 respectively...."
I don't know if this is in the correct category, however it falls within the specialist mathematics field of Australian curriculum and is different to any other Math that I have done before.
Here is my problem:
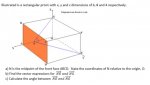
A 3-D box has the dimensions 6, 8 and 4 respectively. A midpoint, N occurs at (6, 4, 2). Find the angle PNQ from point P (0, 0, 4) to Point Q (0, 8, 0).
Using pythagoras and trigonometry I have found the angle as 73.4 degrees. However, I am supposed to use vectors to solve this problem. Any ideas?
I don't know if this is in the correct category, however it falls within the specialist mathematics field of Australian curriculum and is different to any other Math that I have done before.
Here is my problem:
A 3-D box has the dimensions 6, 8 and 4 respectively. A midpoint, N occurs at (6, 4, 2). Find the angle PNQ from point P (0, 0, 4) to Point Q (0, 8, 0).
Using pythagoras and trigonometry I have found the angle as 73.4 degrees. However, I am supposed to use vectors to solve this problem. Any ideas?