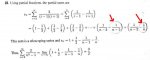2 series questions

[HappyCalculusStudent]

Hello. I've been studying series for the last few weeks.

First, I understand the basics of a telescoping series, but I wasn't sure why the two terms (circled) are not -1/n and -1/(n+1), respectively. I substituted n in place of i directly. Can you show me why the two terms are as written?

Second, I have trouble dealing with factorials. I know you can't consider a function because it's not continuous, but can you ever do a Limit Comparison Test to problems that involve factorials??
For example (I'm modifying a problem that I have),
? ((3^k)+k) / (k !+2)
I'm not sure how to deal with the addition of the two.
I thought about dividing everything by k, but that didn't seem to help.
Could someone give me some hints on how to approach this sort of problem with factorial and addition, please?

 

[galactus]

\(\displaystyle \sum_{k=1}^{\infty}\frac{3^{k}+k}{k!+2}=\sum_{k=0}^{\infty}\frac{3^{k}}{k!+2}+\sum_{k=0}^{\infty}\frac{k}{k!+2}\)

Do you want to prove convergence for this?. Do you want to find what it converges to?

By the limit comparison test, \(\displaystyle \frac{3^{k}+k}{k!+2}<\frac{3^{k}+3^{k}}{k!}=\frac{2(3^{k})}{k!}\),

\(\displaystyle 2\sum_{k=1}^{\infty}\left(\frac{3^{k}}{k!}\right)\) converges by the ratio test:

\(\displaystyle 2\lim_{k\to \infty}\frac{3^{k+1}}{(k+1)!}\cdot \frac{k!}{3^{k}}=2\lim_{k\to \infty}\frac{3}{k+1}=0\)

so \(\displaystyle \sum_{k=1}^{\infty}\frac{3^{k}+k}{k!+2}\) converges.

14.82782755 is what it converges to in case you're interested.

 

[Deleted member 4993]

According to your partial fraction (first line) when i = n

a[sub:19vlteqh]n[/sub:19vlteqh] = 1/(n-1) - 1/(n+1)

when i = n-1

a[sub:19vlteqh]n-1[/sub:19vlteqh] = 1/[(n-1) -1)] - 1/[(n-1)+1] = 1/(n-2) - 1/n

when i = n-2

a[sub:19vlteqh]n-2[/sub:19vlteqh] = 1/[(n-2) -1)] - 1/[(n-2)+1] = 1/(n-2) - 1/(n-1)

So the expansion is shown including a[sub:19vlteqh]n-1[/sub:19vlteqh] (as the last term)- not a[sub:19vlteqh]n[/sub:19vlteqh]

 

[BigGlenntheHeavy]

Note for the first one:
\(\displaystyle S_2 \ can't \ equal \ \frac{2}{3} \ and \ zero \ at \ the \ same \ time, \ ergo \ S_n \ = \ 1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n}, not -\frac{1}{n-1}, \ a \ typo \ in \ your\)
\(\displaystyle book?\)

 

[HappyCalculusStudent]

I didn't think to compare the fraction in that way. That really opens up more possibilities! I think I'll work on some more comparison test problems today, so I get better about seeing things.
Also, it's good to know that the last term in the telescoping series isn't supposed to be for a_n.
I'll go ahead and do more of those examples too.

Thank you all very much!!