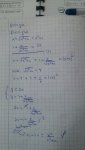2 functions (common tangent in common point): f=x+sqrt{x^2+a}, a>=0; g=x^2+1

[Vali]

The functions from the picture have a common tangent in a common point if:
A. a=1+e
B. a=0
C. a=1
D. a=e-pi
E. a=-1

I know that the conditions are: f(x)=g(x) and f'(x)=g'(x)
I tried to solve the system but I did't get too far.

 

[Dr.Peterson]

The functions from the picture have a common tangent in a common point if:
A. a=1+e
B. a=0
C. a=1
D. a=e-pi
E. a=-1

I know that the conditions are: f(x)=g(x) and f'(x)=g'(x)
I tried to solve the system but I did't get too far.

Please show us the system you tried to solve, and what you tried doing with it, so we can see if it is correct, and maybe suggest what to try next.

 

[Vali]

I tried to make a system then to solve it.I tried to note sqrt(x^2+a)=t but didn't work.Also, I tried to to add what is in left and right then to equal the results but I got no progress.Also,I isolate the sqrt then I square both members and I tried with different "x" (x=0 => a=0 but if x=2 for example the a change it's value).I tried to factorize with Horner scheme.The right answer is B. a=0

 

[Steven G]

I tried to make a system then to solve it.I tried to note sqrt(x^2+a)=t but didn't work.Also, I tried to to add what is in left and right then to equal the results but I got no progress.Also,I isolate the sqrt then I square both members and I tried with different "x" (x=0 => a=0 but if x=2 for example the a change it's value).I tried to factorize with Horner scheme.The right answer is B. a=0

I would 1st try to solve f(x) = g(x)for x, then see if any of those x's satisfies f'(x) = g'(x)

EDIT: Never mind. I did not realize that f is a function of x and a

 

[Dr.Peterson]

I tried to make a system then to solve it.I tried to note sqrt(x^2+a)=t but didn't work.Also, I tried to to add what is in left and right then to equal the results but I got no progress.Also,I isolate the sqrt then I square both members and I tried with different "x" (x=0 => a=0 but if x=2 for example the a change it's value).I tried to factorize with Horner scheme.The right answer is B. a=0

The goal is generally to eliminate one variable.

We have the equations

x + sqrt(x^2 + a) = x^2 + 1
1 + x/sqrt(x^2 + a) = 2x

I first simplified the second by multiplying by the denominator; then I realized I could solve each equation for sqrt(x^2 + a), which is the only place a appears in either equation, and set them equal. This eliminates a and results ultimately in a cubic equation. This can be factored just as you suggest (by recognizing one root by inspection and dividing). Once you have x, you can find a, which is, in fact, 0.

 

[Vali]

I did it
Thank you very much for your help!