Ok, I drew a picture because I couldn't figure out how to explain the diagram. It's not great, but I think it gives you the general idea:
"find x"
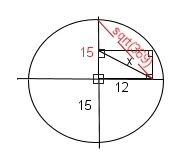
The stuff in black is what I was given, red is what I've filled in. I figured by drawing that red line I could do Pythagorean Theorem, and then prove the triangles similar: The right triangle is in both of them, and they each have a bisected right angle, so they're similar, I believe. Then I can set up a comparison? We've been doing AB/DE = BC/EC = AC/DC, so I thought it might be that. However, I have no idea if that's even remotely on the right track, so before I go any further, can you please tell me if I'm doing it right?
"find x"

The stuff in black is what I was given, red is what I've filled in. I figured by drawing that red line I could do Pythagorean Theorem, and then prove the triangles similar: The right triangle is in both of them, and they each have a bisected right angle, so they're similar, I believe. Then I can set up a comparison? We've been doing AB/DE = BC/EC = AC/DC, so I thought it might be that. However, I have no idea if that's even remotely on the right track, so before I go any further, can you please tell me if I'm doing it right?
