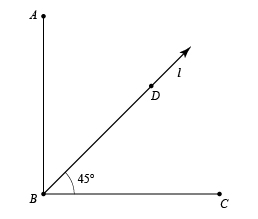
Use the following image to answer the questions below.
a. Based on the picture, what properties can you be sure this figure has? Think about angles, lines, and points.
b. Does ray l
bisect ∠ABC
? Explain your thinking.
c. What would you need to do to prove that ray l
bisects ∠ABC
?
so this is what I answered and I am not sure if i'm right, can someone correct me if i'm wrong. Thanks!
a. In this picture, <abc is a right angle of 90 degrees. There is a bisecting ray, which is an acute angle. Angle abc and angle dbc are adjacent because they share a vertex(B), and a side(BD).
b. Yes, it does, because ray L divides the angle into two different angles. The ray created two acute angles within the right angle.
c. I would need to prove that they both have to equal 90 degrees. One angle is smaller than the other, so by making it equal 90 degrees.
a. In geometry, we are not
sure of anything based on only what it
looks like; we must be able to deduce it from what we are
told. We can't be sure that ∠ABC is a right angle, even though it looks like it; it might be 90.1 degrees, for example. Since they are asking about being
sure, I imagine you have been taught something about that.
What definition have you been given for "adjacent angles"? I would not call ABC and DBC adjacent, but someone else might.
b. It appears to; but you don't know it until you prove it. I don't think you have to prove it here; but you haven't explained your thinking well. Shouldn't the two angles be
equal, rather than "different"? And how does their being acute help?
c. You haven't stated this clearly; what are "they both"??? And do you really mean that
each equals 90, as you have said, or do you mean their
sum? Precision is necessary in proofs.