Definition of Trapezoid

A trapezoid is a quadrilateral with only one pair of parallel sides. As shown in the picture below, the parallel sides of trapezoid ABCD are called bases and the sides that are not parallel are called legs.

Facts About Trapezoids

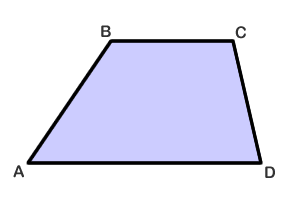
The degree measure of the four angles add up to 360 degrees. This is actually true of any quadrilateral. Let lower case letters a, b, c and d represent the angles of trapezoid ABCD.

The corresponding pairs of base angles, such as A and B, or C and D, are supplementary (add up to 180 degrees).

Isosceles Trapezoid

There is a special kind of trapezoid called an isosceles trapezoid. An isosceles trapezoid is a trapezoid in which the legs are equal in length. Remember that the legs are the non-parallel sides, as opposed to the parallel bases. You'll notice that in the first trapezoid in this lesson (above), the legs are NOT equal.

This is an isosceles trapezoid, called ABCD:

It has the following characteristics:

The two lower base angles have the same measure, and the two upper base angles have the same measure.

The diagonals have the same lengths.

Example Problem

In isosceles trapezoid MATH, side HT is parallel to side MA, line segment MH is congruent to line segment AT. The degree measure of angle MHT = 60 degrees. What are the measures of the other 3 angles?

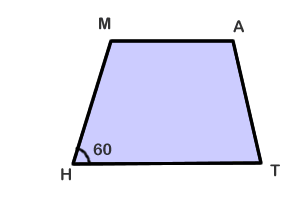
Solution:

We know the two legs are congruent, so this is an isosceles trapezoid. Given that, we know the two base angles (T, H) have the same measure. Because we were given angle H to be 60, we can also say that

Since the top and bottom angles are supplementary, we know that

By the same logic, Angle A = 120 degrees as well.

Lesson provided by Mr. Feliz