Parallel Lines Never Meet

Lines that are in the same plane and do not touch and/or meet are called parallel lines. The notation for parallel lines, , is read: "line AB is parallel to line CD." These lines will continue on forever without crossing.

When two lines are cut by another line, called a transversal, any two of the 8 angles that are formed will equal in measure or will be supplemental:

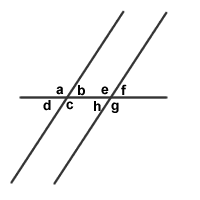
If two lines are cut by a transveral, pairs of angles between the two lines and on opposite sides of the transversal are called alternate interior angles. Alternate interior angles have the same measure, and examples are shown in the color-coded image below:

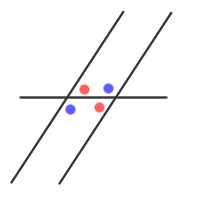
A pair of corresponding angles is made up of one interior angle and one exterior angle both of which are found on the same side of the transveral.

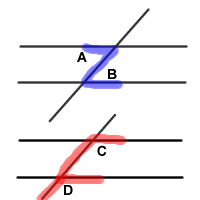
As the pictures below reveal, alternate interior angles form what appears to be a Z-shape and corresponding angles form what appears to be an F-shape:

Properties of Parallel Lines

(1) If two lines are cut by a transversal, pairs of acute angles are equal in measure, pairs of obtuse angles are also equal in measure, and any acute angle is supplementary to any obtuse angle.

If line m is || to line n, then:

(A) Alternate interior angles are equal in measure.

(B) Corresponding angles are equal in measure.

(2) The degree measures of two interior angles on the same side of the transversal will add up to 180.

(3) Also, the sum of the degree measures of any acute angle and any obtuse angle will be 180.

When Are Two Lines Parallel?

Two lines are parallel if any one of the following geometry statements is true:

(A) A pair of alternate interior angles have the same measures.

(B) A pair of corresponding angles have the same measure.

(C) A pair of interior angles on the same side of the transversal are supplementary.

This lesson provided by Mr. Feliz